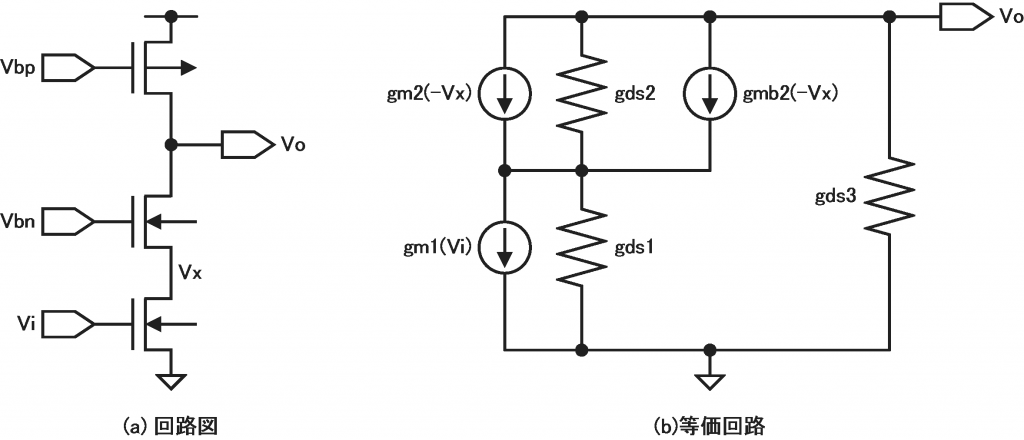
カスコード型は昔ちゃんと計算したことはあったけど、だいぶ忘れてしまったので思い出しがてら再計算してみました。
低周波ゲイン
(1) 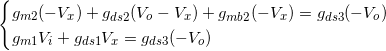
これを計算していくと、![]() と
と![]() の関係は
の関係は
(2) ![]()
となるので、そのまま近似せずゲインを計算すると、
(3) ![]()
ここで、 ![]() が成り立つ場合、
が成り立つ場合、
(4) ![]()
式(4)をよく見ると、ソース接地トランジスタM1の出力インピーダンスが、カスコードトランジスタM2の真性利得倍されていて、これと負荷電流源M3との合成インピーダンスが、この回路の出力インピーダンスになっている事がわかる。
合成インピーダンスなので、![]() がさらに成り立つ場合、式(4)は
がさらに成り立つ場合、式(4)は
(5) ![]()
となり、ゲインは単純にM1の![]() とM3の出力インピーダンスとのかけ算で求められる。
とM3の出力インピーダンスとのかけ算で求められる。
飽和領域動作の条件
M2を飽和領域で動作させる条件は以下の通り。
![]()
M1は以下の通り。
![]()
ここで、![]() の場合、
の場合、
![]()
M3は以下の通り。
![]()